In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends on both the body's speed and its direction of travel. This changing velocity indicates the presence of an acceleration; this centripetal acceleration is of constant magnitude and directed at all times towards the axis of rotation. This acceleration is, in turn, produced by a centripetal force which is also constant in magnitude and directed towards the axis of rotation.
In the case of rotation around a fixed axis of a rigid body that is not negligibly small compared to the radius of the path, each particle of the body describes a uniform circular motion with the same angular velocity, but with velocity and acceleration varying with the position with respect to the axis.
Figure above illustrates velocity and acceleration vectors for uniform motion at four different points in the orbit. Because the velocity v is tangent to the circular path, no two velocities point in the same direction. Although the object has a constant speed, its direction is always changing. This change in velocity is caused by an acceleration a, whose magnitude is (like that of the velocity) held constant, but whose direction also is always changing. The acceleration points radially inwards (centripetally) and is perpendicular to the velocity. This acceleration is known as centripetal acceleration.
For a path of radius r, when an angle θ is swept out, the distance traveled on the periphery of the orbit is s = rθ. Therefore, the speed of travel around the orbit is
 ,
,
The left-hand circle in Figure above is the orbit showing the velocity vectors at two adjacent times. On the right, these two velocities are moved so their tails coincide. Because speed is constant, the velocity vectors on the right sweep out a circle as time advances. For a swept angle dθ = ω dt the change in v is a vector at right angles to v and of magnitude v dθ, which in turn means that the magnitude of the acceleration is given by






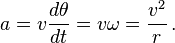



0 comments:
Post a Comment