Saturday, 17 March 2012

Motion with Constant Acceleration

21:18  EC Form6 Physics  No comments

Motion with constant acceleration occurs in everyday life whenever an object is dropped: the object moves downward with the constant acceleration 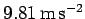$9.81 {\rm m s^{-2}}$, under the influence of gravity.

Fig. 1 shows the graphs of displacement versus time and velocity versus time for a body moving with constant acceleration. It can be seen that the displacement-time graph consists of a curved-line whose gradient (slope) is increasing in time. This line can be represented algebraically as

\begin{displaymath} x = x_0 + v_0 t + \frac{1}{2} a t^2. \end{displaymath} (1)
Here, $x_0$ is the displacement at time $t=0$: this quantity can be determined from the graph as the intercept of the curved-line with the $x$-axis. Likewise, $v_0$ is the body's instantaneous velocity at time $t=0$.
Figure 1: Graphs of displacement versus time and velocity versus time for a body moving with constant acceleration
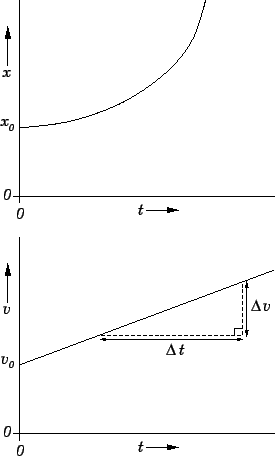\begin{figure} \epsfysize =4.in \centerline{\epsffile{consta.eps}} \end{figure}
The velocity-time graph consists of a straight-line which can be represented algebraically as

\begin{displaymath} v = \frac{dx}{dt}= v_0 + a t. \end{displaymath} (2)
The quantity $v_0$ is determined from the graph as the intercept of the straight-line with the $x$-axis. The quantity $a$ is the constant acceleration: this can be determined graphically as the gradient of the straight-line (i.e., the ratio ${\mit\Delta}v/{\mit\Delta} t$, as shown). Note that $dv/dt=a$, as expected. Equations (1) and (2) can be rearranged to give the following set of three useful formulae which characterize motion with constant acceleration:

$\displaystyle s$ $\textstyle =$ $\displaystyle v_0 t + \frac{1}{2} a t^2,$ (3)
$\displaystyle v$ $\textstyle =$ $\displaystyle v_0 + a t,$ (4)
$\displaystyle v^2$ $\textstyle =$ $\displaystyle v_0^{ 2} + 2 a s.$ (5)

Here, $s=x-x_0$ is the net distance traveled after $t$ seconds. Fig. 2 shows a displacement versus time graph for a slightly more complicated case of accelerated motion. The body in question accelerates to the right [since the gradient (slope) of the graph is increasing in time] between times $A$ and $B$. The body then moves to the right (since $x$ is increasing in time) with a constant velocity (since the graph is a straight line) between times $B$ and $C$. Finally, the body decelerates [since the gradient (slope) of the graph is decreasing in time] between times $C$ and $D$.

Figure 2: Graph of displacement versus time
\begin{figure} \epsfysize =2in \centerline{\epsffile{consta1.eps}} \end{figure}

Posted in:

0 comments:

Post a Comment