In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit time.
Energy transfer can be used to do work, so power is also the rate at which this work is performed. The output power of an electric motor is the product of the torque the motor generates and the angular velocity of its output shaft. The power expended to move a vehicle is the product of the traction force of the wheels and the velocity of the vehicle.
The integral of power over time defines the work done. Because this integral depends on the trajectory of the point of application of the force and torque, this calculation of work is said to be "path dependent."
If ΔW is the amount of work performed during a period of time of duration Δt, the average power Pavg over that period is given by the formula
The instantaneous power is then the limiting value of the average power as the time interval Δt approaches zero.






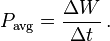




0 comments:
Post a Comment