Equilibrium of a Rigid Body

The Moment of a Force

The moment M (turning effect) of a force about a point O is the product of the magnitude of the force (F) and the perp. distance (x)to the point of application.

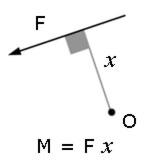
By convention, anti-clockwise moments are positive.

The Principle of Moments

For a rigid body acted upon by a system of coplanar forces, equilibrium is achieved when:

i)  the vector sum of the coplanar forces = 0

ii) there is no net turning effect produced by the forces
(the sum of clockwise & anti-clockwise moments = 0)

Parallel forces acting on a beam

When attempting problems concerning a balance points or fulcrum, remember that there is always an upward force acting.

Example #1   fulcrum near centre

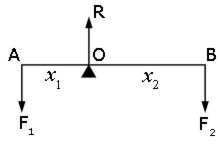
Consider two forces F₁ and F₂ acting vertically downwards at either end of a beam of negligible mass.

When the beam is balanced at its fulcrum O(i.e. horizontal), the sum of the downward forces equals the sum of the upward forces.

If the reaction force at the fulcrum is R,

Example #2   fulcrum at one end

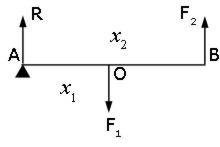
Consider two forces F₁ and F₂ acting on a beam of negligible mass. One force acts vertically downwards near the centre, while the other acts vertically upwards at the end.

When the beam is balanced, the sum of the downward forces equals the sum of the upward forces.

If the reaction force at the fulcrum is R,

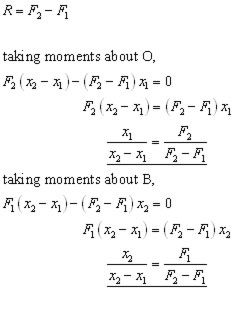
Example #3    a typical problem

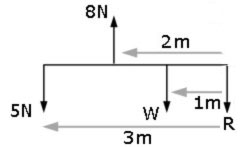
A beam of negligible weight is horizontal in equilibrium, with forces acting upon it, as shown in the diagram.
Calculate the value of the weights R and W.

Couples

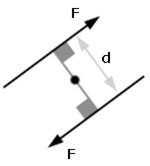
The turning effect of two equal and opposite parallel forces acting about a point equals the product of one force(F) and the perpendicular distance between the forces(d).

couple = F x d

Posted in: