Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path.
In simple terms, centripetal force is defined as a force which keeps a body moving with a uniform speed along a circular path and is directed along the radius towards the centre. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens. Isaac Newton's description was: "A centripetal force is that by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre."
The magnitude of the centripetal force on an object of mass m moving at a speed v along a path with radius of curvature r is:
 is the centripetal acceleration. The direction of the force is toward the center of the circle in which the object is moving, or the osculating circle, the circle that best fits the local path of the object, if the path is not circular. This force is also sometimes written in terms of the angular velocity ω of the object about the center of the circle:
is the centripetal acceleration. The direction of the force is toward the center of the circle in which the object is moving, or the osculating circle, the circle that best fits the local path of the object, if the path is not circular. This force is also sometimes written in terms of the angular velocity ω of the object about the center of the circle:Mass performing vertical circular motion under gravity
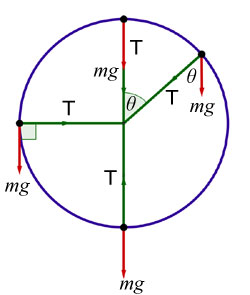
Consider a mass m performing circular motion under gravity, the circle with radius r .
The centripetal force on the mass varies at different positions on the circle.
The centripetal force on the mass varies at different positions on the circle.

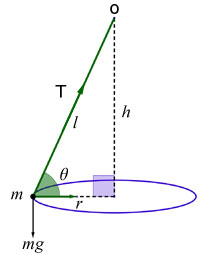
Conical pendulum
Problems concerning the conical pendulum assume no air resistance and that the string has no mass and cannot be stretched.
Solution of problems involves resolving forces on the mass vertically and horizontally. In this way the speed of the mass, the tension in the string and the period of revolution can be ascertained.
Solution of problems involves resolving forces on the mass vertically and horizontally. In this way the speed of the mass, the tension in the string and the period of revolution can be ascertained.
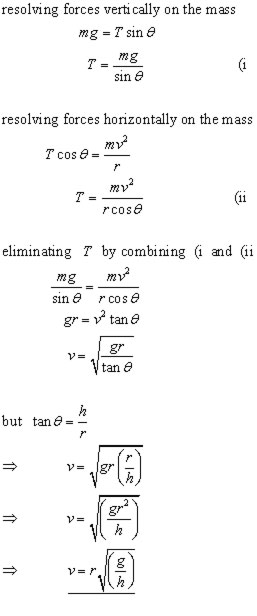







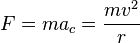





3 comments:
This formula is applicable to the all sports which have circular tracklike cycle racing,motorbike racing.The angle of inclining depends on the velocity and radius.
Chemical Change Examples
Best ias coaching in bangalore
.www.globalias.in
Hello!
Thanks for providing valuable information. on the tipic of Force All the contents are 100% genuine
Post a Comment