Friction is the force opposing the motion of one body sliding or rolling over the surface of second object. Several aspects of friction are important at low velocities:
- The direction of the force of friction is opposite the direction of motion.
- The frictional force is proportional to the perpendicular (normal) force between the two surfaces in contact.
- The frictional force is nearly independent of the area of contact between the two objects.
- The magnitude of the frictional force depends on the materials composing the two objects in contact.
Static friction is the force of friction when there is no relative motion between two objects in contact, such as a block sitting on an inclined plane.
The magnitude of the frictional force is Fs ≤ μs N, where N is the magnitude of the normal force, and the coefficient of friction (μs) is the dimensionless proportionality constant.
The coefficient of friction may be approximately .2 for normal lubricated surfaces and close to 1 for glass sliding on glass. This equation sets the upper limit for the static frictional force. If a greater external force is applied, the situation will no longer be static, and the object will begin to move.
Kinetic friction is the force of friction when there is relative motion between two objects in contact.
The magnitude of the friction force in this case is F k ≤ μk N, where N is the magnitude of the normal force and μ k is the coefficient of kinetic friction. Note that μ k is not strictly a constant, but this empirical rule is a good approximation for finding frictional forces. Values given for the coefficients of static and kinetic friction do vary with speed and surface conditions so that it is not necessarily true that static friction exceeds sliding friction.
The following problem highlights the differences between static and kinetic friction.
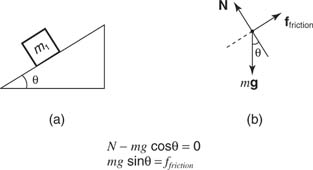
Example 6: A block sits on an inclined plane. What is the maximum angle that which the block remains at rest? First, draw the free-body diagrams and then write out the force equation for each direction of the coordinate system (see Figure 6 ).
| |||
| |||
Suppose the surface is tilted to θ, at which the block just begins to move. Then, the force down the plane must be equal to the maximum force of static friction; thus f friction = μs N. Therefore, f friction = mg sin θ = μs N = μs ( mg cos θ) and solving for the coefficient of friction:
Solution: μs = tan θ
At a greater angle of tilt, the object accelerates down the surface, and the force of friction is f k = μ k N.
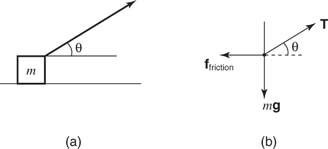
Example 7: If the surfaces in Figures 4 and 5 were not frictionless, the frictional force parallel to the surface and opposite the direction of motion must be included in the analysis. Pulling a block along a horizontal surface at a constant speed (zero acceleration) is an example of a problem involving friction, and such a block is analyzed in Figure 7 .
| |||
| |||
In the x direction, T cos θ − f = 0, where f is the friction force and T is the tension in the rope. In the y direction, N + T sin θ − mg = 0; also, f = μk N.
Solve the y direction equation for N, substitute the expression into the friction force equation, and then substitute friction into the first equation to obtain the following:
|
Solution: 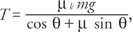 solving for T.
solving for T.
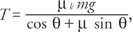 solving for T.
solving for T. 









0 comments:
Post a Comment