In classical mechanics, the kinetic energy of a point object (an object so small that its mass can be assumed to exist at one point), or a non-rotating rigid body, is given by the equation
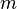 is the mass and
is the mass and 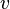 is the speed (or the velocity) of the body. In SI units (used for most modern scientific work), mass is measured in kilograms, speed in metres per second, and the resulting kinetic energy is in joules.
is the speed (or the velocity) of the body. In SI units (used for most modern scientific work), mass is measured in kilograms, speed in metres per second, and the resulting kinetic energy is in joules.When an object is acted upon by conservative forces it can have a potential
energy, U, associated with those forces. Therefore, work also can be defined in terms of the change in potential energy as:
ΔU = −W
In the case of the force due to gravity, the change in potential energy is:
ΔU = −W = mgΔy = mgh
where h is the change in vertical height. The zero point of potential energy is arbitrary, so for convenience it can be set at y = 0. The gravitational potential energy thus becomes:
U = mgy = mgh
The work done by non-conservative forces is equal to the total change in kinetic
and potential energy as given by:
W = ΔK + ΔU
In the special case where no non-conservative forces are acting upon an object, W = 0 and the above equation becomes:
ΔK + ΔU = Δ(K + U) = 0
In other words, the total of the kinetic and potential energy does not change. Thus, the total mechanical energy, E, remains constant and is given by:
E = K + U = constant






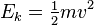



0 comments:
Post a Comment