Rotational motion is more complicated than linear motion, and only the motion of rigid bodies will be considered here. A rigid body is an object with a mass that holds a rigid shape, such as a phonograph turntable, in contrast to the sun, which is a ball of gas. Many of the equations for the mechanics of rotating objects are similar to the motion equations for linear motion.
Angular velocity and angular acceleration
The angular displacement of a rotating wheel is the angle between the radius at the beginning and the end of a given time interval. The SI units are radians. The average angular velocity (ω, Greek letter omega), measured in radians per second, is
|
The angular acceleration (α, Greek letter alpha) has the same form as the linear quantity
|
and is measured in radians/second/second or rad/s2.
The kinematics equations for rotational motion at constant angular acceleration are
|
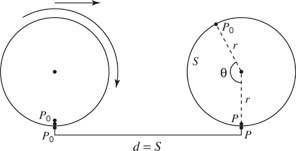
Consider a wheel rolling without slipping in a straight line. The forward displacement of the wheel is equal to the linear displacement of a point fixed on the rim. As can be shown in Figure 1 , d = S = rθ
| |||
| |||
In this case, the average forward speed of the wheel is v = d/ t = ( rθ)/ t = rω, where r is the distance from the center of rotation to the point of the calculated velocity. The direction of the velocity is tangent to the path of the point of rotation.
The average forward acceleration of the wheel is aT = r(ω f − ω o)/ t = rα. This component of the acceleration is tangential to the point of rotation and represents the changing speed of the object. The direction is the same as the velocity vector.
The radial component of the linear acceleration is ar = v2/ r = ω2 r.







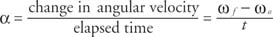
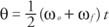
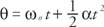



0 comments:
Post a Comment