Substitute Newton's second law into the definition for torque with θ of 90 degrees (a right angle between F and r) and use the relationship between linear acceleration and tangential angular acceleration to obtain t = r F = rma = mr2 ( a/ r) = mr2α. The quantity mr2 is defined as moment of inertia of a point mass about the center of rotation.
Imagine two objects of the same mass with different distribution of that mass. The first object might be a heavy ring supported by struts on an axle like a flywheel. The second object could have its mass close to the central axis. Even though the masses of the two objects are equal, it is intuitive that the flywheel will be more difficult to push to a high number of revolutions per second because not only the amount of mass but also the distribution of the mass affects the ease in initiating rotation for a rigid body. The general definition of moment of inertia, also called rotational inertia, for a rigid body is I = ∑ mi ri2 and is measured in SI units of kilogram-meters2.
| |||
| |||
Mechanics problems frequently include both linear and rotation motions.
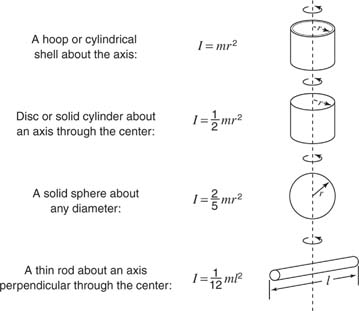
Example 1: Consider Figure 3 , where a mass is hanging from a rope wrapped around a pulley. The falling mass (m) causes the pulley to rotate, and it is no longer necessary to require the pulley to be massless. Assign mass ( M) to the pulley and treat it as a rotating disc with radius (R). What is the acceleration of the falling mass, and what is the tension of the rope?
| |||
| |||
The force equation for the falling mass is T − mg = − ma. The tension of the rope is the applied force to the edge of the pulley that is causing it to rotate. Thus, t = Iα, or TR = (1/2) MR2(a/R), which reduces to T = (1/2) Ma, where angular acceleration has been replaced bya/R because the cord does not slip and the linear acceleration of the block is equal to the linear acceleration of the rim of the disk. Combining the first and last equation in this example leads to
Solution: 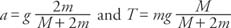
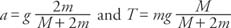









0 comments:
Post a Comment